miércoles, 4 de mayo de 2016

Cargas estáticas.

TEORÍA DE FALLAS PARA MATERIALES FRÁGILES:

Se dice que un material es frágil cuando es muy poca la deformación que presentan antes de romperse. Para este tipo de materiales existen dos teorías, la teoría del máximo esfuerzo normal y el criterio de falla de Mohr.

Teoría de Coulomb-Mohr:
La teoría de Mohr-Coulomb es un modelo matemático  que describe la respuesta de materiales quebradizos, tales como hormigón, o agregados de partículas como el suelo, a esfuerzo cortante, así como tensión normal. La mayoría de los materiales en ingeniería clásica se comportan siguiendo esta teoría al menos en una parte del corte. En general, la teoría se aplica a los materiales para los que la resistencia a la compresión es muy superior a la resistencia a la tracción, caso de los materiales cerámicos. La teoría explica que el corte de un material se produce para una combinación entre tensión normal y tensión tangencial, y que cuanto mayor sea la tensión normal, mayor será la tensión tangencial necesaria para cortar el material. 

El criterio de fallo de Mohr-Coulomb se representa por la envolvente lineal de los círculos de Mohr que se producen en la rotura. La relación de esa envolvente se expresa como:

\tau = \sigma~\tan(\phi) + c
donde:
  • \tau es el esfuerzo cortante.
  • \sigma es la tensión de normal.
  • c es la intersección de la línea de fallo con el eje de \tau, llamada cohesión.
  • \phi es la pendiente del ángulo de la envolvente, también llamado el ángulo de rozamiento interno.
La compresión se asume positiva para el esfuerzo de compresión, aunque también se puede estudiar el caso con la tensión negativa cambiando el signo de \sigma
Si \phi = 0, el criterio de Mohr-Coulomb se reduce al criterio de Tresca. Si \phi = 90^\circ el modelo de Mohr-Coulomb es equivalente al modelo de Rankine. Valores más altos de \phi no están permitidos.
De los círculos de Mohr tenemos:
\sigma = \sigma_m - \tau_m \sin\phi ~;~~ \tau = \tau_m \cos\phi
donde
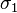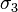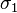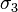\tau_m = \cfrac{\sigma_1-\sigma_3}{2} ~;~~ \sigma_m = \cfrac{\sigma_1+\sigma_3}{2}
y \sigma_1 es la tensión máxima principal y \sigma_3 es la tensión mínima principal.
De esta forma el criterio de Mohr-Coulomb puede expresarse también como:
\tau_m = \sigma_m \sin\phi + c \cos\phi ~.
Esta es la forma del criterio de Mohr-Coulomb aplicable al fallo en un plano paralelo a la dirección \sigma_2.

Teoría de Mohr modificada:
El criterio de Mohr modificado es un criterio de resistencia estática, aplicado a materiales frágiles. Este criterio representa una modificación del criterio de Coulomb-Mohr. El criterio de resistencia se escribe matemáticamente mediante tres condiciones que deben cumplirse para que el punto resista:



donde:
  •  σ1, σ2, σ3 son las tensiones principales en el punto analizado, ordenadas de forma que: 
                
  • Sut>0 es la resistencia a la rotura a tracción, Suc>0  la resistencia a la rotura a compresión
El coeficiente de seguridad en el punto analizado, de acuerdo con el criterio de Mohr modificado se obtiene de:
Este criterio de resistencia puede representarse gráficamente en un diagrama σ1-σ3, como se indica en la figura, representando la zona sombreada la zona segura, para la cual el material resiste de acuerdo con dicho criterio.


Publicadas por a la/s No hay comentarios.:

Cargas estaticas

Teoría de Falla para materiales Dúctiles:

Se considera dúctil a un material que en el ensayo de Tensión haya tenido más del 5% de deformación antes de la fractura. En los materiales dúctiles se considera que la falla se presenta cuando el material empieza a fluir  (falla por deformación).Cuando se somete un elemento a una carga de tracción libre, cualquier punto de este queda sometido a un estado de esfuerzo uniaxial, el máximo esfuerzo normal actúa en la dirección de la fuerza y el máximo esfuerzo cortante en planos inclinados 45º con esta dirección. Si se somete un material dúctil a una carga de tracción, el material falla debido a la acción de los esfuerzos cortantes, ya que en la rotura se tiende a formar un cono cuya generatriz forma generalmente 45º  con la dirección axial, entonces serian los esfuerzos cortantes los culpables de los desplazamientos  de los cristales cuando se alcanza el límite de fluencia, los cristales siguen deslizándose sobre la red hasta la rotura.
Sin embargo entre los materiales dúctiles se encuentran la mayoría de los metales y plásticos poliméricos. Se debe tener presente que en términos generales, los materiales dúctiles tienen la misma resistencia a la tracción y a la compresión y no son tan susceptibles a las zonas de concentración de tensiones en términos comparativos con los materiales frágiles. Se puede considerar que un material dúctil ha fallado cuando en términos globales la tensión que está soportando alcanza la tensión de fluencia.
Ejemplo Un suelo falla cuando pierde permanentemente  su capacidad para soportar esfuerzos debido a una carga externa (el peso de una edificación, el empuje lateral de una estructura, entre otros). Si el suelo se deforma notoriamente antes de fallar, es un suelo que presentara  una falla dúctil; es decir, fallara después de deformarse en una buena medida.

Teoría del esfuerzo normal máximo:
La Teoría del Esfuerzo Normal Máximo (TENM), o teoría del esfuerzo principal máximo, fue expresada por  W.J.M.Rankine y data del año 1850 aproximadamente. Solo se presenta por interés histórico ya que no es adecuada para materiales frágiles ni dúctiles.   Esta teoría establece que la falla suele ocurrir siempre que el esfuerzo principal mayor sea igual a la resistencia del material. O también cuando el esfuerzo normal en la probeta llegue a cierto límite de la resistencia normal, como puede ser el límite de fluencia elástico a tensión o la resistencia máxima a tensión del material. Para el caso de materiales dúctiles, el criterio deseado es la resistencia límite. 

La falla ocurrirá en la parte di cualquiera de los esfuerzos normales principales excede el esfuerzo normal principal que da lugar a la falla en la prueba uniaxial simple.

Si:        S1 = Esfuerzo Principal 1                   syc = Esfuerzo de fluencia a compresión
            S2 = Esfuerzo Principal 2                  syt = Esfuerzo de fluencia a tensión.
            S3 = Esfuerzo Principal 3.

Teoría del esfuerzo cortante máximo:
Siempre da predicciones seguras, se utiliza únicamente para predecir fluencia y, por lo tanto, se aplica solo a los materiales dúctiles.
Esta teorÍa afirma que el fallo (por fluencia) empieza cuando, en un elemento mecánico, el esfuerzo cortante máximo llega a ser igual al esfuerzo cortante máximo en una probeta a tensión, cuando este espécimen empieza a ceder. Así, en el caso de tensión pura de un espécimen normalizado para el ensayo de tensión, la fluencia empieza cuando

Tao(max) = Sy / 2.

Para fines prácticos, un diseño es seguro cuando


          Tao(max) = Sy / 2*n


Donde: n= factor de seguridad
             Sy = resistencia a la fluencia
             Tao(max) = esfuerzo cortante máximo.
 

Como es de esperarse, esta teoría predice que la resistencia de fluencia al cortante está dada por la ecuación.
 
                      Ssy = 0.50 Sy

Teoría de la energía de distorsión:
Este criterio puede considerarse un refinamiento del criterio de Tresca. El criterio de la máxima energía de distorsión fue formulado primeramente por Maxwell en 1865 y más tarde también mencionado por Huber (1904). Sin embargo, fue con el trabajo de Richard Edler von Mises(1913) que el criterio alcanzó notoriedad, a veces se conoce a esta teoría de fallo elástico basada en la tension de  Von Mises  como teoría de Maxwell+-Huber-Hencky-von Mises. La expresión propuesta por Von Mises y Hencky, de acuerdo con este criterio una pieza resistente o elemento estructural falla cuando en alguno de sus puntos la energía de distorsión por unidad de volumen rebasa un cierto umbral:
e_{\rm dist} \ge \frac{\sigma_Y^2}{2E}
En términos de tensiones este criterio puede escribirse sencillamente en términos de la llamada tensión de von Mises como:
\sigma_{\rm vM} = \sqrt{\frac{(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2 +(\sigma_3-\sigma_1)^2}{2}} \ge \sigma_Y
Donde:
\sigma_1 \ge \sigma_2 \ge \sigma_3\;  son las tensiones principales en el punto considerado.
Publicadas por a la/s No hay comentarios.:

lunes, 4 de mayo de 2015

Algunos elementos del buque sometidos a cargas estaticas

https://gastonperezu.files.wordpress.com/2011/10/unefa-sin-fondo.pngRepública Bolivariana de Venezuela
Ministerio del Poder Popular para la Defensa
Universidad Nacional Experimental de la Fuerza Armada
 Nacional Bolivariana
Núcleo Sucre – Sede Cumaná
















Elementos Sometidos a Cargas Estáticas






















Profesor:                                                                                                             Alummna:
Cesar Castañeda                                                                                          Noelka Urbaez
                                                                                                                     C.I:20403170

Diseño de elementos sometidos a cargas estáticas:

Dentro de las diferentes fallas que se pueden encontrar  en un buque pueden ser, por sobrecarga, fallos de diseño, mano de obra en la construcción, vibraciones, uso y desgaste.
Muchos los factores que  pueden contribuir a fallas estructurales en un buque de acero, pero las más recurrentes son: edad del buque, fatigas, corrosión.

Edad del Buque
Este es uno de los factores más importantes a tener en cuenta tanto en la búsqueda de defectos como en la decisión más económica de su reparación. “El mismo defecto podría tener un tratamiento diferente según la edad del buque”.

Corrosión:
La corrosión se acelera en aquellas zonas donde hay una tensión local mayor que en las zonas que la rodean. Esto ocurre fundamentalmente donde el agente causante de la corrosión esta presente casi en forma continua, por ejemplo tanque de lastre sin protección. Este fenómeno se presenta en forma reiterativa ya que cuando existe mayor tensión inicial en una zona que en las adyacentes, aumenta la corrosión local. Al disminuir el espesor por el aumento de corrosión, provoca a su vez aumento de tensión o sea: a mayor tensión mayor es la corrosión y a mayor corrosión mayor va a ser la tensión.
Fatiga:
La fatiga en materiales puede definirse como un fallo bajo cargas repetidas o la
Propagación de una grieta a través de un componente debido a un sistema de
Cargas de naturaleza cíclica. Estas cargas pueden ser muy inferiores a la carga de rotura. La fractura por fatiga, la cual es una falla que progresa lentamente durante un largo periodo de tiempo, puede ser producida por tensiones de tracción o compresión, o una combinación de ambas.

Algunos elementos estructurales que presentan fallas por cargas estáticas en un buque son:

Estructura de cubierta:
El tramo de cubierta existente entre dos escotillas se ve sometido a esfuerzos de torsión y/o fuerzas producidas por cargas laterales, especialmente si el soporte bajo la cubierta es un mamparo corrugado, el lugar en el que la concentración de estos esfuerzos es mayor esta situado en las esquinas de las escotillas (sobre todo si existen grandes diferencias de espesores entre las planchas que las configuran) y las de las brazolas.

Estructura del doble fondo:
Las zonas más comunes donde se pueden presentar grietas se producen, como en tantas ocasiones se ha señalado, en los cordones de soldaduras existentes entre el doble fondo y una consola o también una tolva baja, sobre todo si existen problemas de alineación entre estas en los refuerzos bajo el doble fondo, cuando el espaciado de estos refuerzos es mayor que el adecuado o cuando la groeras existentes entre el doble fondo, el longitudinal correspondiente y la plancha inclinada de la tolva (para bulkcarrier) es mayor de lo debido para el simple paso del cordón de soldadura. Para la formación de una tolva no se utiliza soldadura sino que se usa una plancha plegada, también es frecuente de que aparezcan grietas en esta zona del codillo y en el centro de su radio de curvatura
El doble fondo es la zona de grandes probabilidades de grietas y corrosiones, especialmente en buques de cierta antigüedad.

Raseles proa y popa:
El principal problema de estas zonas deriva de la falta de pintura en los raseles o bien por la carencia de mantenimiento de la que se aplico inicialmente. En el caso del pique de popa, otra de las posibles causas de grietas puede proceder de la vibración resultante de la excitación de la hélice, que puede generar fracturas tanto en los refuerzos del rasel como en el propio forro. La fuerte estructura de estas zonas puede verse muy afectada es caso de colisión pudiendo llegarse a agrietar de forma importante los mamparos de colisión o de popa de maquinas según sea el caso.

Mamparos transversales y estructuras asociadas:
Los mamparos transversales pueden ser de tres tipos: Corrugados, de doble plancha o planos con refuerzos verticales. En los primeros casos pueden o no llevar polines o bancadas de apoyo en su parte superior y/o inferior.


Forro, cuadernas y pies de consola:
Esta corrosión afecta de manera especial a la unión de las cuadernas con las consolas, sobre todo si esas zonas carecen de pintura. El resultado puede ser el desprendimiento del refuerzo de la chapa y grietas en las consolas y cuadernas. Es importante observar que la disminución de espesores por corrosión en los refuerzos puede pasar desapercibida si no se elimina de estos la capa de oxido que eventualmente puede cubrirlos. Generalmente los problemas no vienen solos sino que se agrupan, de esta forma hay que considerar que estos se pueden multiplicar si coinciden zonas de corrosión, fatiga y deformaciones a l mismo

Publicadas por a la/s No hay comentarios.:

Teoría para el tema a estudiar



DISEÑO DE ELEMENTOS SOMETIDOS A CARAGAS ESTATICAS:
Una carga estática es aquella que no varía su magnitud y dirección en el tiempo.

Teoría de fallas para materiales
La falla es la perdida de función de un elemento  tanto por deformación (fluencia) como por la separación de sus partes (fractura). Los mecanismos de falla dependen de la estructura microscópica del material y de las formas de sus enlaces atómicos. Para predecir las fallas de materiales bajo cargas estáticas y poder hacer diseños de elementos de maquinas confiables se han desarrollado varias teorías para grupos de materiales, basándose en observaciones experimentales
Las fallas se clasifican en dos: materiales dúctiles y frágiles. Hablaremos de los materiales dúctiles.
Teoría de falla para materiales dúctiles:
Se considera dúctil a un material que en el ensayo de Tensión haya tenido más del 5% de deformación antes de la fractura. En los materiales dúctiles se considera que la falla se presenta cuando el material empieza a fluir  (falla por deformación).Cuando se somete un elemento a una carga de tracción libre, cualquier punto de este queda sometido a un estado de esfuerzo uniaxial, el máximo esfuerzo normal actúa en la dirección de la fuerza y el máximo esfuerzo cortante en planos inclinados 45º con esta dirección. Si se somete un material dúctil a una carga de tracción, el material falla debido a la acción de los esfuerzos cortantes, ya que en la rotura se tiende a formar un cono cuya generatriz forma generalmente 45º  con la dirección axial, entonces serian los esfuerzos cortantes los culpables de los desplazamientos  de los cristales cuando se alcanza el límite de fluencia, los cristales siguen deslizándose sobre la red hasta la rotura.
Sin embargo entre los materiales dúctiles se encuentran la mayoría de los metales y plásticos poliméricos. Se debe tener presente que en términos generales, los materiales dúctiles tienen la misma resistencia a la tracción y a la compresión y no son tan susceptibles a las zonas de concentración de tensiones en términos comparativos con los materiales frágiles. Se puede considerar que un material dúctil ha fallado cuando en términos globales la tensión que está soportando alcanza la tensión de fluencia.
Ejemplo Un suelo falla cuando pierde permanentemente  su capacidad para soportar esfuerzos debido a una carga externa (el peso de una edificación, el empuje lateral de una estructura, entre otros). Si el suelo se deforma notoriamente antes de fallar, es un suelo que presentara  una falla dúctil; es decir, fallara después de deformarse en una buena medida.
Teoría del esfuerzo normal máximo
La Teoría del Esfuerzo Normal Máximo (TENM), o teoría del esfuerzo principal máximo, fue expresada por  W.J.M.Rankine y data del año 1850 aproximadamente. Solo se presenta por interés histórico ya que no es adecuada para materiales frágiles ni dúctiles.   Esta teoría establece que la falla suele ocurrir siempre que el esfuerzo principal mayor sea igual a la resistencia del material. O también cuando el esfuerzo normal en la probeta llegue a cierto límite de la resistencia normal, como puede ser el límite de fluencia elástico a tensión o la resistencia máxima a tensión del material. Para el caso de materiales dúctiles, el criterio deseado es la resistencia límite. 
Teoría de la máxima tensión cortante

La teoría de la máxima tensión cortante fue introducida en forma independiente por Coulomb (1773) y por Tresca (1868), y se la suele llamar también Criterio de Fluencia de Coulomb- Tresca o Criterio de Fluencia de Tresca. De acuerdo con la evidencia experimental sobre laminas de titanio y otros metales, según las cuales los mismos se deformaban según planos de corte perfectamente definidos. Estas observaciones condujeron a definir el criterio de fluencia como sigue: Una pieza sujeta a cualquier combinación de cargas sufrirá falla cuando la tensión cortante máxima exceda un valor crítico. El valor crítico se puede obtener a partir de los ensayos de tracción y compresión convencionales. 




Publicadas por a la/s No hay comentarios.:
Suscribirse a: Entradas (Atom)